O mundo dos labirintos sempre fascinou a humanidade, desde os antigos mitos gregos até os modernos quebra-cabeças. Recentemente, físicos do Reino Unido e da Suíça levaram esse fascínio a outro nível, criando o que muitos consideram o labirinto mais difícil do mundo.
A origem do labirinto
O projeto foi liderado por Felix Flicker, físico da Universidade de Bristol, juntamente com Shobhna Singh da Universidade de Cardiff e Jerome Lloyd da Universidade de Genebra. A equipe se inspirou em conceitos da geometria fractal e no movimento do Cavalo no xadrez para criar um labirinto extremamente complexo.
LEIA MAIS: Você conhece o lugar mais silencioso do mundo? Veja o que ele faz com você!
Eles utilizaram padrões conhecidos como mosaicos de Ammann-Beenker para gerar rotas chamadas ciclos hamiltonianos, resultando em labirintos fractais intrincados.
Você pode ver a seguir um labirinto gerado de acordo com os preceitos acima (a resposta vamos deixar no final do texto). Lembrando que a estrutura pode se tornar tão maior e complexa quanto se queira:
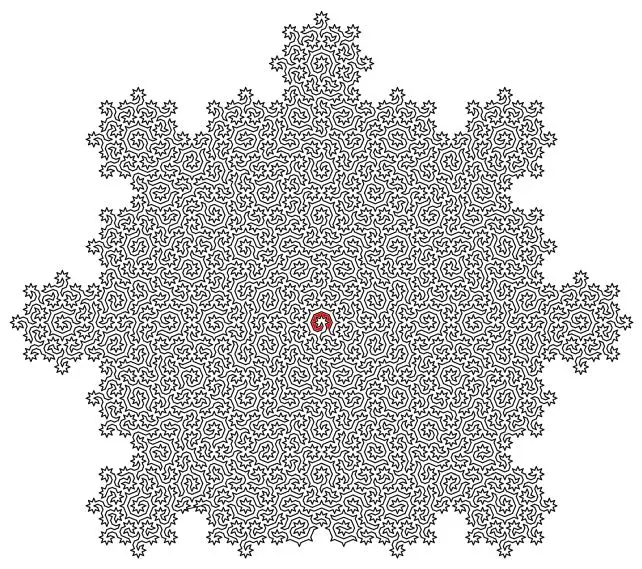
Créditos: Universidade de Bristol
A Geometria Fractal
A geometria fractal foi essencial para a criação deste labirinto. Fractais são padrões matemáticos que se repetem em diferentes escalas, e no caso deste labirinto, cada parte do caminho reflete a complexidade do todo.

Exemplo de fractal
Essa característica torna o labirinto realmente bem difícil e, ao mesmo tempo, fascinante, sob o ponto de vista visual e matemático.
O conceito de ciclos Hamiltonianos
Um ciclo hamiltoniano, por sua vez, é uma rota que passa por cada ponto de um mapa apenas uma vez antes de retornar ao ponto de partida. No contexto do labirinto mais difícil do mundo, isso significa que cada caminho dentro do labirinto é único e não se repete.
Esses ciclos foram gerados usando mosaicos de Ammann-Beenker, padrões matemáticos que não se repetem de forma idêntica, semelhante aos quasicristais encontrados na natureza.
Quasicristais e mosaicos aperiódicos
Quasicristais são uma forma exótica de matéria na qual os átomos formam padrões que parecem se repetir, mas não o fazem perfeitamente. Isso contrasta com cristais ordenados, como o sal ou o diamante, onde os padrões atômicos são perfeitamente repetitivos.

Exemplo de estrutura de quasicristal
A utilização de quasicristais na criação do labirinto permitiu a formação de caminhos ímpares e extremamente complexos, onde cada parte menor do labirinto se assemelha à maior, criando um fractal infinito.
LEIA MAIS: Turbulências em voos: como mudanças climáticas afetam as viagens aéreas?
Aplicações práticas da pesquisa
Embora a criação deste labirinto possa parecer uma curiosidade científica, a pesquisa tem aplicações muito mais amplas que apenas essa.
A descoberta de ciclos hamiltonianos em quasicristais pode ajudar na solução de problemas complexos em várias áreas, como a descoberta de rotas em sistemas complexos e o enovelamento de proteínas.
Além disso, a pesquisa sugere que os quasicristais podem ser mais eficazes que os cristais tradicionais em processos de adsorção, como na captura de carbono, devido à sua estrutura irregular e maior área de superfície.
Interessante, não é?
Resposta do Labirinto
Uma das respostas possíveis apresentada pelos cientistas da Universidade de Bristol é a seguinte:
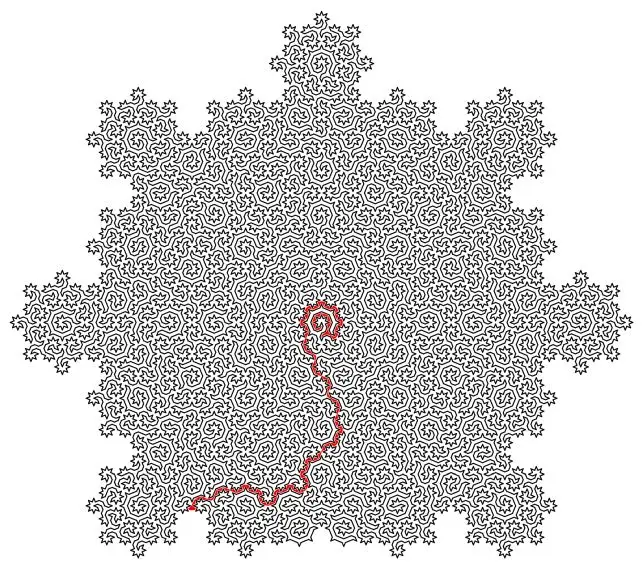
Créditos: Universidade de Bristol













0 comentários